参考 ·https://article.itxueyuan.com/RdR53m ·https://blog.csdn.net/lemonxiaoxiao/article/details/108619552 ·https://www.cnblogs.com/HolyChen/p/5982184.html ·https://oi-wiki.org/geometry/rotating-calipers/
问题引入
给定一个多边形S,寻找该多边形直径,即寻找它们之间有最大距离的一对点 。
前置知识
凸包
假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。
支撑线
直线 (L) 过凸多边形 (P) 一个顶点,使 (P) 全在 (L) 一侧,此时称直线 (L) 为凸多边形 (P) 的支撑线。
对踵点
两条平行直线过凸多边形的两个顶点且将凸多边形夹在其之间,此时这对顶点称作对踵点。
两条平行支撑线所过两点是一对对踵点。
凸多边形直径定理
凸多边形 (P) 的直径 (=) 凸多边形 (P) 的所有平行支撑线之间距离的最大值。
算法描述
Graham Scan法
用以寻找凸包。
它的时间复杂度与所采用的排序算法时间复杂度相同,通常采用线性对数算法,因此为 O ( N l o g ( N ) ) O(Nlog(N)) O ( N l o g ( N ) )
找到所有点P 0 , 1 , . . . , N − 1 P_{0,1,...,N−1} P 0 , 1 , . . . , N − 1 最下方的点 ,记为P L P_L P L
计算所有其他的点P i ( i ≠ L ) P_i(i≠L) P i ( i = L ) P L P_L P L P L P i → \overrightarrow{P_LP_i} P L P i P L P_L P L
对所有其他的点按照第2步算出的角度进行排序,且P L P_L P L
从点P L P_L P L
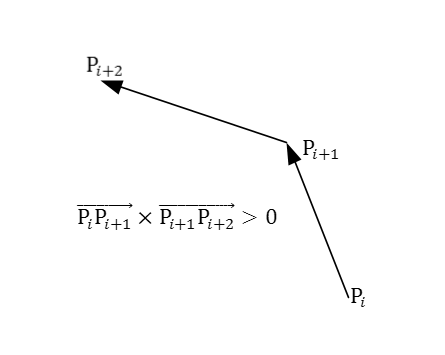
判断三个点依此连成两条线段走向是否为逆时针,用这两条线段向量的叉积(即叉乘)判断:叉积>0,逆时针;反之顺时针或者共线。
附上部分代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 from math import *n = int (input ()) a = [] l = 0 for i in range (n): m = list (map (float ,input ().split())) a.append(m) '''----------开始寻找凸包-------------''' a = sorted (a,key = lambda x:x[1 ]) print (a)x1,y1 = 1 ,a[0 ][1 ] for i in range (len (a)): if i == 0 : a[i].append(0 ) else : x2,y2 = a[i][0 ]-a[0 ][0 ],a[i][1 ]-a[0 ][1 ] cosx = (x2+y2*y1) / (sqrt(x1**2 +y1**2 )*sqrt(x2**2 +y2**2 )) a[i].append(cosx) a[1 :] = sorted (a[1 :],key = lambda x:(-x[2 ])) print (a)i = 2 while i < len (a): x1,y1 = a[i-1 ][0 ]-a[i-2 ][0 ],a[i-1 ][1 ]-a[i-2 ][1 ] x2,y2 = a[i][0 ]-a[i-1 ][0 ],a[i][1 ]-a[i-1 ][1 ] if (x1*y2)-(x2*y1) > 0 : i += 1 else : del a[i-1 ] print (a)
旋转卡壳法
寻找凸多边形对踵点的算法。
主要思路:利用凸包单调性,枚举点 -> 更新点对 -> 更新答案。
求出凸多边形凸包。此时最远点对必在凸包上,时间复杂度为 O ( N l o g ( N ) ) O(Nlog(N)) O ( N l o g ( N ) )
找到一对初始对踵点,作水平切线。y m a x y_{max} y m a x y m i n y_{min} y m i n
沿一个方向旋转这两条切线,直到其中一条与凸包的边重叠。
该算法本质上是对于每一条凸包的边,计算最远的过凸包上点的平行直线。
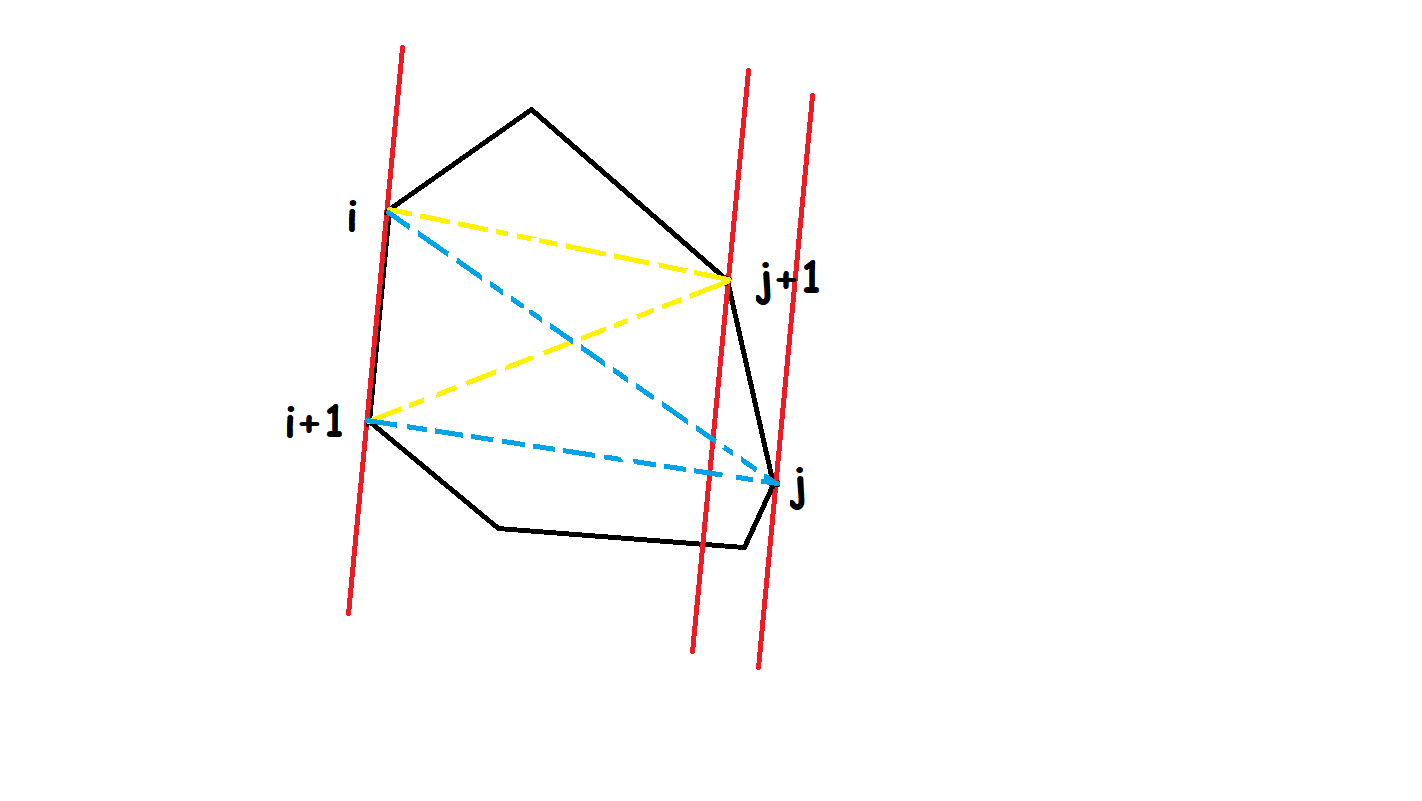
注意: 求出凸包后的数组自然地是按照逆时针旋转的顺序排列,不过要记得提前将最左下角的 i i i ( i , i + 1 ) (i,i+1) ( i , i + 1 )
j + 1 j+1 j + 1 ( i , i + 1 ) (i,i+1) ( i , i + 1 ) i i i j j j j j j
例题: https://matiji.net/exam/brushquestion/373/3846/4C6668FEB8CFD6520DE73B365B31D1A4
附上代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 from math import *def sqr (i, j, a ): x1 = a[i][0 ] - a[i-1 ][0 ] y1 = a[i][1 ] - a[i-1 ][1 ] x2 = a[j][0 ] - a[i-1 ][0 ] y2 = a[j][1 ] - a[i-1 ][1 ] return abs (x1*y2-x2*y1) n = int (input ()) a = [] l = 0 temp = 0 for i in range (n): m = list (map (float ,input ().split())) a.append(m) a.append(a[0 ]) xymax = max (a,key= lambda x:x[1 ]) ymax = xymax[1 ] xymin = min (a,key= lambda x:x[1 ]) ymin = xymin[1 ] l = ymax - ymin j = 2 for i in range (1 ,n+1 ): x1 = a[i][0 ] - a[i-1 ][0 ] y1 = a[i][1 ] - a[i-1 ][1 ] while sqr(i,j,a) <= sqr(i,j % n + 1 ,a): j = j % n + 1 x2 = a[j][0 ] - a[i-1 ][0 ] y2 = a[j][1 ] - a[i-1 ][1 ] x3 = a[j][0 ] - a[i][0 ] y3 = a[j][1 ] - a[i][1 ] l1 = max (sqrt(x2**2 +y2**2 ),sqrt(x3**2 +y3**2 )) l = max (l,l1) print ("{:.6f}" .format (l))
OvO